Pulley Pressures
Notes & Use
Calculates:
- D:d ratios for given pulley and cable sizes
- Tread pressure
- Pressure exerted on the groove by the load
- Wrap angle is taken into account, see image
- A round cable is assumed
- A properly-sized round groove is assumed, the nominal groove diameter is approximately:
$$ D_{groove} = 1.06 \times D_{cable} $$ - Note that the tread pressure as depicted in the figure below is not technically accurate, but more illustrative in nature. The tread pressure is actually calculated as the force acting on the cross-sectional midplane of the sheave such that: $$ \frac {Force} {Diameter_{cable} \times Diameter_{tread}} $$
- Bore pressure
- Pressure exerted on the shaft bore by the load
- Note that the bore pressure as depicted in the figure below is not technically accurate, but more illustrative in nature. The bore pressure is actually calculated as the force acting on the cross-sectional midplane of the bore such that: $$ \frac {Force} {width_{bore} \times Diameter_{bore}} $$
Figure
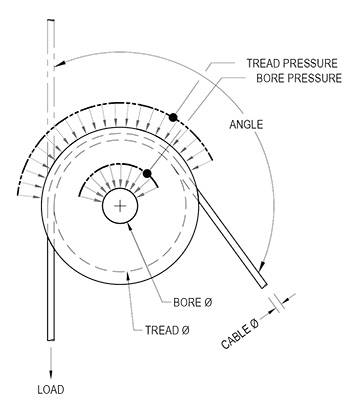
Terms
$L$ = Load, pounds force
$D_{tread}$ = Tread diameter, inches
$D_{cable}$ = Cable diameter, inches
$D_{bore}$ = Bore diameter, inches
$w$ = width at bore, inches
$\phi$ = angle of wrap around the sheave, degrees.
Where:
- φ ≥ 0°
- φ < 180°
Equations
Pitch Diameter, inches: $$ D_{pitch} = D_{tread} + D_{cable}$$
D:d ratio, unitless: $$ D:d = \frac {D_{pitch}} {D_{cable}} $$
Calculate the resultant force on the sheave, lbf:
$$ F_{resultant} = 2 L \, cos \, \left( \frac {180 - \phi}{2} \right) $$
Tread pressure, psi:
$$ P_{tread} = \frac {F_{resultant}}{D_{tread} D_{cable}} $$
Bore pressure, psi:
$$ P_{bore} = \frac {F_{resultant}}{w \, D_{bore}} $$
Sources
Nylatron Tech Report. H&H Specialties, Inc., 2004.
Stage Rigging Handbook. Jay O. Glerum, 23rd ed, pp 12-13.